Soovime näiteks kontrollida, kas tudengite seas on mehi ja naisi võrdselt, kas tudengite seast ühte juhuslikult välja noppides saame tõenäosusega 0,5 kätte naistudengi. Vaatame esmalt, palju olemasolevas andmestikus on naistudengeid (tunnuse sugu kodeering: 1-naine; 2-mees):

table(sugu)

Tulemus:

   sugu
     1   2 
   512 149 

Näeme, et kokku vaatlesime 512 naistudengit (meid huvitav sündmus toimus 512 korda) ja kokku vaadeldi 512+149=661 tudengit (katsete - üks katse on ühe tudengi noppimine tudengite populatsioonist - koguarv). Kontrollimaks, kas juhuslikult kõigi tudengite seast ühte noppides on naistudengi saamise tõenäosus 0,5 (ehk kas naisi ja mehi on tudengite seas võrdselt) saame järgmise käsu abil:

binom.test(512, 512+149, p=0.5)

Tulemus:

        Exact binomial test

data:  512 and 512 + 149
number of successes = 512, number of trials = 661, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.7407839 0.8059101
sample estimates:
probability of success 
              0.774584 

Näeme, et nullhüpotees (H₀: p=0,5) tuleb kummutada, nullhüpoteesi väide pole kooskõlas olemasolevate andmetega (sest p-value < 2.2e-16 ehk p-väärtus on väiksem kui 0,00000000000000022, see aga on märksa väiksem kui tavapärane olulisuse nivoo 0,05. Seega ei saa nullhüpoteesi väide olla õige).

Usaldusintervall tõenäosusele näitab, et naistudengite tegelik osakaal uuritavas populatsioonis on 95% kindlusega vahemikus 74%...81% (95 percent confidence interval: 0.7407839 0.8059101; ehk tegelik tõenäosus asub üsna kindlasit vahemikus 0,74078...0,80591).

• Kuidas usaldusintervalle joonisele (tulpdiagrammile) kanda, vaata siit.
  
• Usaldusintervallide lisamist sagedustabelitesse vaata aga siit.
  

Kui soovime leida tavapärase 95%-usaldusintervalli asemel mõnda teist usaldusintervalli, näiteks 80%-usaldusintervalli, siis tuleb käsule lisada conf.level= lisaparameeter:

binom.test(512, 512+149, conf.level=0.8)

Tulemus:

        Exact binomial test

data:  512 and 512 + 149
number of successes = 512, number of trials = 661, p-value < 2.2e-16
alternative hypothesis: true probability of success is not equal to 0.5
80 percent confidence interval:
 0.7523986 0.7955349
sample estimates:
probability of success 
              0.774584 

Kas uuritava tunnuse jaotus on selline, nagu väidab meile teooria? Oletame, et ristame heterosügootseid vanemaid Aa x Aa ja vaatame laste genotüüpe. Kui uuritav lookus päranduks Mendeli seadustele vastavalt, siis ootaksime, et 1/4 järglastest oleks genotüübiga AA; 1/2 järglastest peaks olema genotüübiga Aa ja 1/4 järglastest genotüübiga aa. Meie tehtud ristamiskatses oli aga AA genotüübiga järglaseid 13, heterosügootseid järglasi (Aa) 23 ja genotüübiga aa järglasi 10. Kas võiksime sedavõrd veidrat valimit kohata siis, kui antud lookus päranduks Mendeli seadustele vastavalt? Seda saame kontrollida chisq.test käsu abil (mis teeb hii-ruut testi). Kontrollitava teooria poolt väidetavad erinevate katsetulemuste esinemistõenäosused antakse ette p= lisaparameetri abil (tõenäosused peavad olema samas järjekorras kui väärtuste esinemissagedused):

chisq.test(c(13, 23, 10), p=c(1/4, 2/4, 1/4))

Tulemus:

        Chi-squared test for given probabilities

data:  c(13, 23, 10)
X-squared = 0.3913, df = 2, p-value = 0.8223

Teine näide

Keegi poliitik on öelnud, et tänapäeva tudengitest 2/3 on naised ja 1/3 meestudengid. Kontrollime seda väidet tudengite andmestiku peal. Esmalt vaatame, millises järjekorras esitatakse sagedusi sagedustabelis (tunnus sugu oli kodeeritud 1-naine, 2-mees):

table(sugu)

sugu
  1   2 
512 149 

chisq.test(table(sugu), p=c(2/3, 1/3))

Tulemus:

        Chi-squared test for given probabilities

data:  table(sugu)
X-squared = 34.6415, df = 1, p-value = 3.964e-09

Kuna p-väärtus tuli väike (3.964e-09=0,000000003964), siis saame tõestada, et poliitiku väide ei pea paika, poliitik valetas (alternatiivne võimalus: meil pole tegemist korrektselt võetud valimiga ehk valim pole esindav - algandmed mida kasutame on valed).

Hii-ruut testi kasutamisnäiteid hüpoteeside kontrollimiseks pideva uuritava tunnuse kohta vaata siit.

Vahel arvame teadvat uuritava tunnuse jaotust. Näiteks heterosügootsete vanemate ristamisel (Aa x Aa) võiksime näha tõenäosusega 0,25 järglast genotüübiga AA, tõenäosusega 0,5 järglast genotüübiga Aa ja järglast genotüübiga aa tõenäosusega 0,25. Kui kavatseme uurida oma projekti raames 100 heterosügootsete vanemate last, siis keskeltläbi võiks meie valimisse sattuda 25 genotüübiga AA järglast. Aga on üsnagi ebatõenäoline, et 100-st sündivast lapsest oleksid täpselt 25 genotüübiga AA. Ikka võib juhtuda, et sünnib mõni AA-genotüübiga laps kas rohkem või vähem... aga kui palju siis võiks ikkagi genotüübiga AA järglaseid 100 lapse seas leiduda? Sellele küsimusele vastamiseks vajame prognoosiintervalli.

Liigume prognoosiintervalli leidmise juurde sammhaaval. Käsu

qbinom(0.025, prob=0.25, size=100)

[1] 17

tulemus ütleb meile, et kui kordame sama katset sõltumatult 100 korda ühe katse õnnestumise tõenäosus on aga 0,025 ehk 25%, siis vaid 2,5% sellistest 100-katselistest seeriatest annab tulemuse, kus õnnestunud katseid oli 17 või vähem. Järgmise käsu abil näeme, et enamike 100-katseliste katseseeriate korral (97,5% katseseeriatest) näeme 34 või vähem õnnestumist (kui katse õnnestumise tõenäosus on 0,25):

qbinom(0.975, prob=0.25, size=100)

[1] 34

Seega jääb vähemalt 95% katseseeriate korral õnnestunud katsete arv 100-katselise katseseeria korral vahemikku 17..34 (kui ühe katse õnnestumise tõenäosus on 0,25 ja katseid sooritatakse teineteisest sõltumatult). Olemegi leidnud 95%-prognoosiintervalli õnnestuvate katsete arvule (ehk AA-genotüübiga järglaste arvule kui vaatleme 100-t heterosügootsete vanemate järglast).

Kui kavatseme uurida 100 heterosügootsete vanemate järglast, siis nendest peaks heterosügootseid (genotüübiga Aa) järglaseid olema:

qbinom(c(0.025, 0.975), prob=0.5, size=100)

[1] 40 60

Programm, mis joonistab prognoosiintervalle iseloomustava joonise:

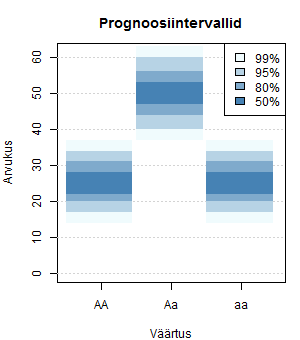
toenaosused=c(0.25, 0.5, 0.25)
nimed=c("AA","Aa","aa")
katseid=100

mitu=length(toenaosused)
plot(NA, NA, xlim=c(0, mitu), 
   ylim=c(0,katseid*max(toenaosused)+
      2.3*sqrt(katseid*max(toenaosused)*
        (1-max(toenaosused))) ), 
   xaxt="n", xlab="Väärtus", 
   main="Prognoosiintervallid", ylab="Arvukus") 

# Lisame referentsjooned (abijooned)
grid(ny=NULL, nx=0)

for (i in 1:mitu){
   p=toenaosused[i]

   # Arvutame vajalikud prognoosiintervallid:
   # 99%-prognoosiintervall
   vahe1=qbinom(c(0.005, 0.995), prob=p, size=katseid)
   # 95%-prognoosiintervall
   vahe2=qbinom(c(0.025, 0.975), prob=p, size=katseid)
   # 80%-prognoosiintervall
   vahe3=qbinom(c(0.1, 0.9), prob=p, size=katseid)
   # 50%-prognoosiintervall
   vahe4=qbinom(c(0.25, 0.75), prob=p, size=katseid)

   # Kanname leitud prognoosiintervallid graafikule ristkülikutena:
   rect((i-1), vahe1[1], i-0.05, vahe1[2], col="azure", border=NA)
   rect((i-1), vahe2[1], i-0.05, vahe2[2], col="lightblue1", border=NA)
   rect((i-1), vahe3[1], i-0.05, vahe3[2], col="deepskyblue", border=NA)
   rect((i-1), vahe4[1], i-0.05, vahe4[2], col="midnightblue", border=NA)
}

# Lisame alla teljele väärtuste tähistused
axis(1, at=(1:i)-0.5, nimed)

# Lisame legendi
legend("topright", fill=c("azure","lightblue1", "deepskyblue", "midnightblue"), 
	c("99%","95%", "80%", "50%"), bg="white")