Advendikalendri lahendused

4. detsember

10% Jõulumaa töötajatest töötavad tislerina, kus nad saavad praegu Jõulumaa keskmist palka. Päkapikkude nõukogu tahab tõsta tislerite palka nii, et pärast palgatõusu saaksid nad Jõulumaa keskmisega võrreldes kahekordset palka.

Mitu korda tuleb tislerite palka suurendada?

Lahendus

Olgu K₁ esialgne Jõulumaa töötajate keskmine palk. Kuna 10% Jõulumaa töötajatest töötavad tislerina, ja 90% kellegi muuna, siis saab esialgse keskmise palga arvutuse kirjutada välja järgmiselt:

0.1 K_{1} + 0.9 K_{1} = K_{1} .

Olgu K₂ keskmine palk pärast palgatõusu. Pärast palgatõusu saavad tislerid keskmisega võrreldes kahekordset palka ehk 2K₂. Uue keskmise palga arvutuse saab välja kirjutada järgmisel kujul:

0.1 \cdot 2 K_{2} + 0.9 K_{1} = K_{2} .

Leiame

\frac{2 K_{2}}{K_{1}} .

0.9 K_{1} = (0.5 - 0.1) 2 K_{2} \Rightarrow \frac{2 K_{2}}{K_{1}} = \frac{0.9}{0.4} = 2.25

Seega tuleb tislerite palka suurendada 2.25 korda.

5. detsember

Päkapikk Juss unustas salajase jõululao koordinaadid. Samas on Jussil meeles, et need koordinaadid olid seotud ühe erilise 10-kohalise arvuga. See arv on selline, et arvu esimene number tähistab nullide arvu selles arvus, teine number ühtede arvu ja nii edasi kuni viimase numbrini, mis tähistab üheksate arvu.

Leia selline 10-kohaline arv.

Lahendus

Kuna otsitav arv on 10-kohaline ja iga number näitab numbrite arvu, siis otsitava arvu ristsumma on võrdne kümnega.

Proovimise ja välistamise teel on võimalik saada vastuseks 6210001000. (See on ainukene nõutud tingimustele vastav arv.)

Näiteks otsitavast arvust saab lihtsalt välistada numbrid 9, 8 ja 7. Kui number 9/8/7 ei ole esimene number, siis saaks näidata, et ristsumma on kümnest suurem. Kui number 9/8/7 on esimene number, siis peab olema 10./9./8. number nullist erinev ning 1/2/3 numbrit nullist erinevad. On lihtne kontrollida, et jõuame vastuoluni.

6. detsember

Kaks lumehelbekest said kokku ning otsustasid mängida äraarvamismängu. Mängu reeglid on sellised, et mõlemad valivad arvu ühest kolmekümneni (1,2,...,30) ja esitavad kumbki kaks küsimust, millele teine peab vastama ausalt parima teadmise järgi.

Nende vestlus kõlas nii:
LH1: Lumehelbeke, kas sinu arv on 2 korda suurem kui minu arv?
LH2: Ei tea. Lumehelbeke, kas sinu arv on 2 korda suurem kui minu arv?
LH1: Ei tea. Lumehelbeke, kas sinu arv on 2 korda väiksem kui minu arv?
LH2: Ei tea. Lumehelbeke, kas sinu arv on 2 korda väiksem kui minu arv?
LH1: Ei tea.
LH2: Siis ma tean, mis su arv on!

Millise arvu valis esimene lumehelbeke?

Lahendus

Kuna LH2 ei tea LH1 arvu, siis esimesele küsimusele võimalikud vastused on "ei" juhul kui LH2 arv ei ole üheski arvust kaks korda suurem või "ei tea" (ehk "võib-olla") juhul kui leidub arv, millest LH2 arv on kaks korda suurem. Analoogselt on võimalik vastata ülejäänud küsimustele.

Saame teada, et LH2 arv on paaristarv.
LH1: -
LH2: 2,4,6,...,30
Saame teada, et LH1 arv jagub neljaga.
LH1: 4,8,12,...,28
LH2: 2,4,6,...,30
Saame teada, et LH2 arv on väiksem kui 15.
LH1: 4,8,12,...,28
LH2: 2,4,6,...,14
Saame teada, et LH1 arv on väiksem kui 7.
LH1: 4
LH2: 2,4,6,...,14

Seega on vastuseks 4.

7. detsember

Päkapikkude töökojas on võrdkülgse kolmnurga kujuline tuba. Päkapikud soovivad osta põrandale uue punase vaiba, aga nad ei ole kindlad, kui suure pindalaga vaipa neil vaja on. Nad teavad, et nende lilla vaiba pindala on 4 ruut-päka-meetrit. Lilla ja rohelised vaibad on täisnurksed kolmnurgad.

Kui suure pindalaga vaipa vajavad päkapikud?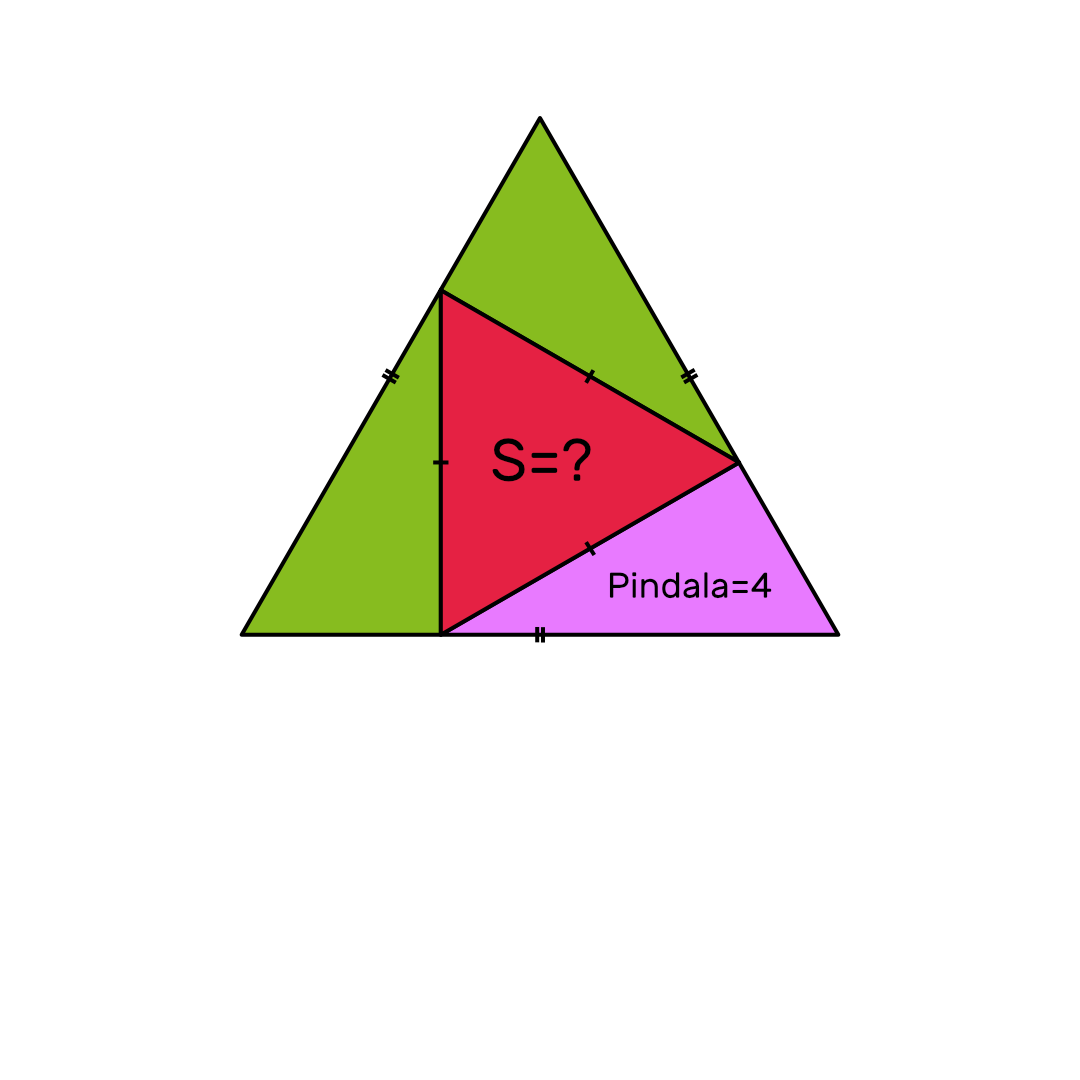 Ülesannet kirjeldav pilt

Lahendus

Roheline kolmnurk on pool võrdkülgsest kolmnurgast, mille külje pikkus on 1.5 korda väiksem kui suure võrdkülgse kolmnurga pindala. Punase kolmnurga pindala on (1.5²⋅2-3) 4 = 6 ruut-päka-meetrit.

8. detsember

Päkapiku ühikas on 30 voodikohta. Päkapikk Juss on hajameelne ning pärast pikka tööööd jääb täiesti juhuslikul voodil magama. Ülejäänud päkapikud tulevad ükshaaval sisse ja üritavad esmalt minna oma voodisse. Kui see on aga hõivatud, siis valivad päkapikud juhusliku vaba voodi.

Kui suur on tõenäosus, et viimasena ühikasse naasev päkapikk saab oma voodisse?

Lahendus

Viimase päkapiku saatus on niipea teada kui keegi on läinud tema voodisse või Jussi voodisse. Tähistame tähega A sündmust "Viimane päkapikk saab oma voodisse" ja tähistusega B_n sündmust "n-s päkapikk läheb Jussi voodisse või viimase päkapiku voodisse". Paneme tähele, et P(A | B_n)=½.

Kasutades law of total probability saame, et P(A) = P(A | B₁) P(B₁) + ... + P(A | B₃₀) P(B₃₀) = ½ [P(B₁) + ... + P(B₃₀)] = ½.

9. detsember

Päkapikk Juss laenas päkapikk Maia lahtritega sahtlist nööpe. Päkapikk Maia on väga süsteemne ning tahab, et sahtel oleks samasuguses seisus nagu enne. Kahjuks Juss ei mäleta, mitu nööpi ühes lahtris esialgu oli. Kas saad Jussi aidata?

Mis arv peaks olema allolevas tabelis ? asemel?

Lahendus

Tegu on ülesandega, kus võib mitmeid erinevaid mustreid leida ja kui suuta neid põhjendada, siis ükski nendest ei ole tingimata vale. Tavaliselt selliste ülesannete puhul hinnatakse parimateks lahenditeks neid, mis on kõige lihtsamal kujul. Lihtsus on subjektiivne. Lugesime õigeks järgmisi lahendusi:

Kui 1. veerg on x ja 3. veerg on y, siis 2. veerg oleks 12x + 5y. Nii oleks vastuseks 53.
4. rida = 1. rida * 2. rida - 3.rida. Nii oleks vastuseks 2453.

10. detsember

Jõulumeeleolus jõulumemm kinkis oma 80-pealisele päkapikumeeskonnale 10x8 šokolaaditahvli. Päkapikud otsustasid selle tahvli omavahel võrdselt jagada nii, et igaüks saab 1x1 suuruse tüki. Šokolaadi murdmine on aga vaevarikas töö.

Millisel viisil saab šokolaaditahvli vähima arvu kordadega murda 1×1 tükkideks? Tõesta!

Murda saab ainult ühte tahvlit korraga ja ainult mööda ruutudevahelisi sirgjooni.

Lahendus

Ei ole vahet kuidas me šokolaaditahvlit murrame. Igal murdmisel me suurendame tükkide arvu ühe võrra ning lõpus on 80 šokolaaditükki.

11. detsember

Jõuluvana nägi unes üht erilist lukustusmehanismi, mida tal nüüd väga vaja on. Selleks pöördub ta Sinu poole, et Sa aitaksid tal selle välja mõelda.

Maas on kolm vaia ning Sinu ülesandeks on panna köis ümber kolme vaia nii, et kui eemaldada ainult üks vai, siis köis on kahe posti küljes kinni, aga kui eemaldada ükskõik millised kaks vaia, siis köis vabaneb.

Sõlme kirjapaneku meetodi kohta saab lugeda siit.

Lahendus

Sõlmedega mängides võib tähele panna, et

kui meil on sõlm ümber vaiade, siis seda saab panna kirja erinevat moodi, sõltuvalt alguspaiga asukohast sõlmel ja alguspaigast liikumise suunast. See, et erinevate alguspaikatega saame sama sõlme, tähendab näiliselt seda, et nt. sõlmed abbc, bbca, bcab ja cabb on samad.
kui järjest teha a ja a', siis see on samaväärne sellega, et me teeme mitte midagi ehk aa'=O.
tähti a,a',b,b',c,c' ei saa kuidagi muud moodi taandada või ümber tõsta kui kahes eelnevas punktis mainitud viisil
eemaldades 1.,2. või 3. vaia eemaldame sõlme kirjeldusest vastavalt tähed a,a' või b,b' või c,c'.

Seega sobib lahendiks näiteks abca'b'c', sest kui näiteks eemaldame 1. vaia, saame sõlme bcb'c' ja siis eemaldades 2. vaia saame cc'=O ehk köis vabaneb. Teistmoodi vaiasid eemaldades saame sama tulemuse.

Matemaatikutele: Sõlmede kirjapanekul on sellised omadused (eelnevas loetelus 2. ja 3. punkt), sest tasand millest on eemaldatud lõplik arv punkte on homotoopiline sidusa graafiga ning sidusa graafi fundamentaalrühm on vaba rühm.

12. detsember

Aednik-päkapikk Herbert tahab oma peenralt seened välja ajada. Herberti peenar koosneb kolmest ruudukujulisest platsist, mis on alloleval joonisel märgitud punaselt. Igal platsil paikneb üks seen. Peenraväline ala, mis on joonisel valget värvi, on lõpmatu ruudustik.

Seentel on eriline omadus: kui neid puudutada, siis nad poolduvad, kusjuures üks pool liigub ühe ruudu võrra üles ning teine pool liigub ühe ruudu võrra paremale. See tähendab, et esialgne ruut muutub tühjaks. Samas kui seenest üleval või paremal paikneval ruudul on juba seen ees, siis seen ei pooldu üldse ning jääb paigale.

On teada, et nurgas paiknev seen kaalub 1 kg ning tema kõrval paikevad kaks seent kaaluvad ½ kg.

Mitme puudutusega on võimalik seened Herberti peenralt välja saada? Ülesannet kirjeldav pilt

Lahendus

Seente mass oli antud vihjeks järgmisele lahenduskäigule. Kui jälgime, mis massiga seened mis ruutudel olla saavad, siis näeme, et ruudul (i,j) saavad olla ainult seened massiga 2^-i-j kg.

Oletame, et kogu ruudustik on seentega kaetud. Ruudustiku esimese rea seente mass on leitav geomeetrilise reana 1+1/2+1/4+...=2. Iga järmise rea mass on eelmisest 1/2 korda väiksem. Saame, et kogu ruudustiku mass on 2+1+1/2+...=4. Punase ala mass on 2 ja seega on ülejäänud ala mass ka 2. Järeldub, et lõpliku arvu puudutustega ei ole võimalik seeni punaselt alalt välja saada.

13. detsember

Laanes elavad viis oravat ning üks käbilind. Oravad ajasid päeva jooksul ühiselt kokku suure käbihunniku.

Öösel, kui teised oravad magasid, ärkas esimene orav üles ning plaanis enda võrdse osa varakult oma peidukohta viia. Orav jaotas käbihunniku viieks võrdseks osaks ning ühe üle jäänud käbi viskas uudistavale käbilinnule. Kui orav oli oma osa ära peitnud lükkas ta teised käbid tagasi ühte hunnikuse ning heitis magama.

Ükshaaval ärkasid ka järgmised oravad. Oravad jaotasid samamoodi ühise hunniku viieks võrdseks osaks, viskasid ühe käbi käbilinnule, peitsid oma osa ära, lükkasid käbikuhja kokku ning heitsid magama.

Hommikuks oli käbihunnik ilmselgelt pisemaks jäänud. Kuna olukord oli piinlik, ei maininud nad midagi ning jagasid käbid omavahel võrdselt ära. Seekord ei jäänud ühtegi käbi üle.

Kui palju käbisid oli esialgses käbihunnikus? Esita vähim võimalik käbide arv.

Lahendus

Vastus: 3121

Näitame, et see on tõepooles vähim võimalik lahend. Olgu x₀ esialgne käbide kogus ning x₁,...,x₅ käbide kogus hunnikus pärast öised jagamisi. Jagamise protsessi kirjeldab seos $x_{i + 1} = 4 (x_{i} - 1) / 5 .$

Kuna $4 (x_{i} - 1) / 5 = 4 (x_{i} + 4) / 5 - 4$ , siis saame võrduse $5 (x_{i + 1} + 4) = 4 (x_{i} + 4),$ millest järeldub $5^{5} (x_{5} + 4) = 4^{5} (x_{0} + 4) .$

Vähim võimalik x₀ väärtus on 5⁵-4=3121 ja vähim võimalik x₅ on 4⁵-4. Hommikune jagamine on võimalik, sest 4⁵-4=4(4²+1)(4²-1) jagub viiega.

14. detsembri mõistatus

Päkapikk Juss läks külla oma sõbrale nöpsik Miale. Mia on selle poolest eriskummaline sõber, et ta elab kahemõõtmelises maailmas. Nöpsikud on tolle maailma päkapikud.

Pärast teed ja küpsiseid otsustasid Juss ja Mia mängida paari lauamängu. Mängiti ühemõõtmelist kabet ning ühemõõtmelist malet.

Ühemõõtmelist kabet mängitakse 1x8 laual, kus positsioonidel 1,2,3 on valged nupud ning positsioonidel 6,7,8 mustad. Mäng käib nagu klassikaline kabe mäng ikka, ainult et justkui kogu tegevus toimuks 8x8 kabelaua diagonaalil.
Ühemõõtmelist malet mängitakse 1x8 laual, kus positsioonidel 1,2,3 on vastavalt valge kuningas, ratsu ja vanker ning positsioonidel 8,7,6 on must kuningas, ratsu ja vanker. Mängureeglid on nagu maleski. Kuningas saab liikuda ühe ruudu võrra, ratsu peab liikuma kahe ruudu võrra, aga saab teistest nuppudest üle hüpata ning vanker saab liikuda mitme ruudu võrra - nagu maleski. Vangerdada ei saa. Ühemõõtmelises males kehtivad malemängu mõisted tuli, matt ja patt.

Kuna päkapikk Juss tunneb, et tal on kolmemõõtmelise olendina eelis, siis ta annaks mängude alustuskorra põhjal eelise nöpsik Miale.

Kui mängijad mängivad ratsionaalselt, siis kas ühemõõtmelises kabes võidab alustaja (valge) või 2. mängija (must)? Aga ühemõõtmelises males?

Lahendus

Ühemõõtmelises kabes võidab 2. mängija (must). Esimesed viis käiku on kohustuslikud. Edasises mängus kaotab see, kes teeb esimesena agressiivse käigu.

Ühmõõtmelises males võidab 1. mängija (valge). Lahendust näeb ja saab proovida lehel https://rowan441.github.io/1dchess/chess.html.

15. detsembri mõistatus

Olgu meil 2023x2023 ruudustik.
Mitu ruutu esineb sellises ruudustikus (1x1, 2x2, 3x3, ..., 2023x2023 ruutu)?

Lahendus

Vastus on

1^{2} + 2^{2} + 3^{2} + . . . + 2023^{2} = \frac{2023 \cdot (2023 + 1) \cdot (2 \cdot 2023 + 1)}{6} = 2761775324.

Ruutude summat kirjeldatvat kuuppolünoomi on võimalik leida näiteks Newtoni ritta arendamise teel.