Tõenäosuspaber - võrdlus teoreetilise jaotusega
q-q plot
Sisuline interpretatsioon ja tunnetuslikke näiteid

Pahatihti kerkib üles küsimus, kas mingi tunnuse jaotuseks on mingi tuttav teoreetiline jaotus. Näiteks: uuritava tunnuse jaotust soovitakse võrrelda normaaljaotusega (sest kasutatav meetod eeldab normaaljaotusega tunnust); paljude testide p-väärtuste jaotust soovitakse võrrelda ühtlase jaotusega (kui kõigi testide puhul kehtis nullhüpotees, siis peaksid p-väärtused olema ühtlase jaotusega (parameetriliste testide korral); soovime teada, kas tööstusseadmete eluead on eksponentjaotusega vms. Valimi jaotuse võrdlemiseks teoreetilise jaotusega on enamkasutatavaks jooniseks tõenäosuspaber ehk kvantiil-kvantiil graafik (q-q plot).

Tõenäosuspaberi graafiku selgitus: vaadatakse valimi (0,5/n)-kvantiili (valimi miinimum), (1,5/n)-kvantiili (suuruselt järgmine vaatlus peale valimi miinimumi), ... , ((n-0,5)/n)-kvantiili (valimi maksimum). Nende kvantiilidega pannakse kokku teoreetilise jaotuse (0,5/n)-kvantiil, (1,5/n)-kvantiil, ..., ((n-0,5)/n)-kvantiil. Vastavaid teoreetilisi kvantiile võib interpreteerida (ligikaudu) ka nii: kui suur võiks olla suurim vaatlus antud suurusega valimis, kui uuritava tunnuse jaotus on selline nagu me arvame ta olevat jne.

Kui uuritava tunnuse tegelikuks jaotuseks on meie poolt kahtlustatav teoreetiline jaotus, siis peaksid teoreetilised kvantiilid ja valimi kvantiilid olema sarnased ja punktid (x=teoreetiline kvantiil; y=valimi kvantiil) peaksid ligikaudu paiknema ühel sirgel. Kui tõenäosuspaberile kantud punktid kalduvad süstemaatiliselt kõrvale sirgest, siis võib kahtlustada, et uuritava tunnuse jaotus erineb väljapakutud jaotusest.

Võrdlus normaaljaotusega
Normaaljaotuse korral pole erilist vahet, kas võrdleme valimikvantiile andmetele kõige paremini sobiva normaaljaotuse kvantiilidega või standardse normaaljaotuse N(0;1) kvantiilidega - kui uuritav tunnus on normaaljaotusega, peaksid mõlemal graafikul punktid (teoreetiline kvantiil; valimi kvantiil) paiknema ühel sirgel. Sestap võrreldaksegi normaaljaotuse eelduse kontrollimisel sageli valimi kvantiile standardse normaaljaotuse kvantiilidega, nii nagu seda teeb ka R kui kasutada käsku qqnorm:

qqnorm(kaal)

# lisame abijoone
qqline(kaal)

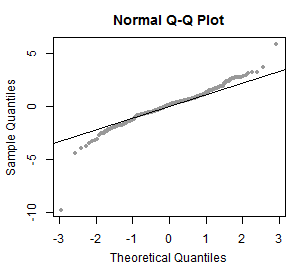
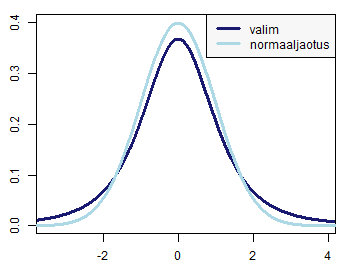
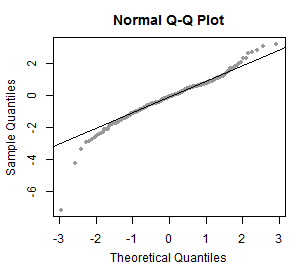
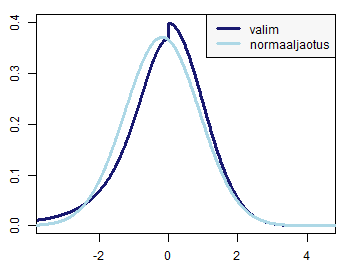
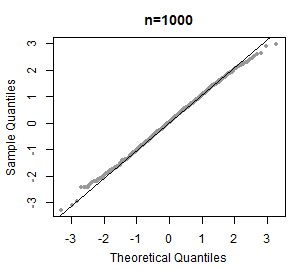
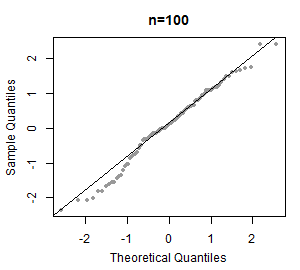
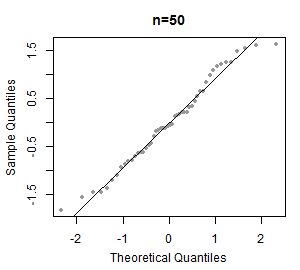
Nende käskude tulemusel saadud jooniselt võib näha, et punktid ei paikne isegi ligilähedaselt sirgel - võime selle joonise põhjal järeldada, et tudengite kaalude jaotus pole normaaljaotusega.

Formaalse testi normaaljaotuse kontrollimiseks võid leida siit.

Näiteid normaaljaotuse jaoks tehtud tõenäosuspaberitest ja nende selgitusi:

Ekstreemselt suuri ja ekstreemselt väikeseid väärtuseid leidub rohkem kui normaaljaotuse korral peaks esinema (jaotusel on liiga rasked sabad)
Ekstreemselt suuri väärtuseid leidub rohkem kui normaaljaotuse korral peaks esinema (jaotusel on raske saba paremal)
Väga väikeseid väärtuseid leidub rohkem kui ootaksime normaaljaotuse korral (jaotusel on raske saba vasakul)
Väga suuri ja väga väikeseid väärtuseid esineb vähem kui normaaljaotuse korral eeldaksime (jaotusel on kerged sabad)
Tunnuse tegelikuks jaotuseks on normaaljaotus
Tunnuse tegelikuks jaotuseks on normaaljaotus


Võrdlus teiste jaotustega
Kui soovime joonistada graafikut kontrollimaks, kas olemasolevad vaatlused võiksid olla pärit mingist konkreetsest teoreetilisest jaotusest (mis pole normaaljaotus), siis peame joonise tegemiseks ise leidma kontrollitava jaotuse sobivad kvantiilid. Paljude jaotuste jaoks on R'is olemas funktsioonid, mis leiavad antud jaotuse kvantiile. Ühtlase jaotuse kvantiile saab leida näiteks funktsiooniga qunif, eksponentjaotuse kvantiile käsuga qexp, Poissoni jaotuse kvantiile saab leida käsuga qpois jne. 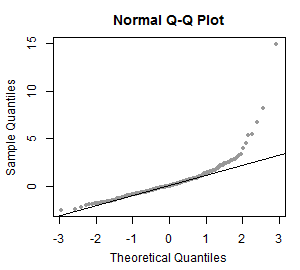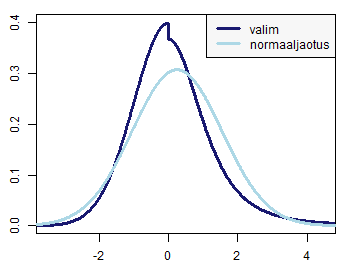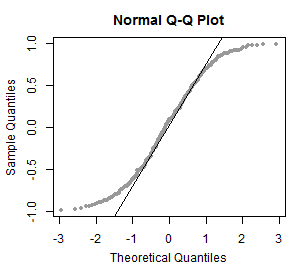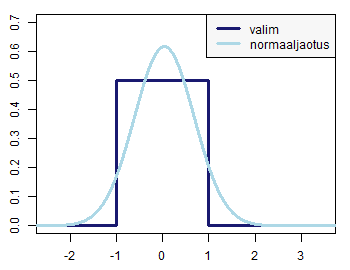R-le teadaolevaid jaotusi ja nende jaotuste kvantiilide leidmiseks vajalike funktsioonide nimed leiad kui palud R-is abiinformatsiooni jaotuste kohta (?Distributions).

Alljärgnevalt vaatame joonist, mis kontrollib, kas tunnuses vaatlused olevad väärtused (mis antud näites on genereeritud) ikka võiks olla pärit ühtlasest jaotusest:

# Algandmed - illustreerimiseks kasutame genereeritud algandmeid,
# tavaliselt peaks olema tunnuses vaatlused need väärtused, mille jaotust
# soovitakse testida.
vaatlused=runif(150)

# Joonistame tõenäosuspaberi tunnuses "vaatlused" olevatele vaatlustele: qqplot(qunif(ppoints(vaatlused)), vaatlused, pch=20, col="gray50")
abline(coef=c(0,1))
Saadud graafiku interpretatsioon on sanane varasemale - kui uuritava tunnuse jaotus on selline nagu arvame (st. kui antud näites vaatlused on pärit ühtlasest jaotusest) - siis peaksid graafikule kantud punktid paiknema enam-vähem ühel sirgel. Antud juhul paiknevadki punktid ligikaudu sirgel, seega võime oletada, et uuritava tunnuse jaotuseks on ühtlane jaotus (või ühtlasele jaotusele väga sarnane jaotus). Tegemist on muidugi õige järeldusega, sest antud näite jaoks genereerisimegi vaatlused ühtlasest jaotusest.

Kui soovid graafikule lisada ka mõne formaalse statistilise testi poolt leitud p-väärtuse (mis kontrollib, kas uuritava tunnuse jaotus ikka on selline nagu sa arvasid), siis vaata siia.