Naase kalendri juurde
Naase kalendri juurde

Päkapikud pakivad jõulukinke. Nende produktiivsus sõltub sellest, kui palju päkapikke koos töötavad. Kui 5 päkapikku suudavad pakkida 100 kinki 4 tunniga, siis oletame, et iga päkapiku efektiivsus järgib pöördvõrdelist sõltuvust päkapike arvust.
Ühe päkapiku efektiivsus: 100/(5 × 4) = 5 kinki tunnis.
10 päkapiku puhul väheneb iga päkapiku efektiivsus: 5/2 = 2.5 kinki tunnis.
10 päkapiku koguefektiivsus: 10 × 2.5 = 25 kinki tunnis.
Kokku pakitakse 4 tunni jooksul: 25 × 4 = 100 kinki.
Ühe päkapiku efektiivsus: 5 kinki tunnis (nagu esimese küsimuse lahenduses).
8 päkapiku puhul väheneb igaühe efektiivsus: 5 × (5/8) = 25/8 ≈ 3.125 kinki tunnis.
8 päkapiku koguefektiivsus: 8 × 3.125 = 25 kinki tunnis.
Aeg 100 kingi pakkimiseks: 100/25 = 4 tundi.
10 päkapikku pakivad 4 tunni jooksul 100 kingitust. 8 päkapikku pakivad 100 kingitust 4 tunniga.
Traditsioonikohaselt on ka sel aastal oravad ajanud kokku ühe suure käbihunniku. Viis oravat otsustasid saagiks saadud käbihunniku omavahel võrdselt ära jagada, kuid alles pärast rajudast oravate jõulupeost väljapuhkamist.
Öösel ärkab üks oravatest üles ja jaotab käbid võrdselt viide hunnikusse. Selle käigus jääb üks käbi üle, mille ta viskas minema. Seejärel peidab ta ühe hunnikutest ja paneb ülejäänud neli tagasi ühte suurde hunnikusse.
Sama teevad ka ülejäänud oravad teineteise järel. Hommikul, kui nad hakkavad käbisid võrdselt jagama, jääb üks käbi jälle üle.
Mis on väikseim käbide arv, mille oravad algselt kokku ajasid?Tähistagu T(x) käbide arvu, mis jääb järele pärast jagamist kuhjast, milles oli x käbi. T(x) = (4/5)(x - 1). Nimetame täisarvu x vastuseks, kui arvule x funktsiooni T kuus korda järjest rakendades saame tulemuseks täisarvu. Peame leidma vähima naturaalarvulise vastuse.
Kuna T(x) = (4/5)x - 4/5, siis:
T6(x) = (4/5)6x - ((4/5)6 + (4/5)5 + … + 4/5)),
mistõttu:
T6(x) - T6(y) = (4/5)6(x - y),
iga x ja y korral. See tähendab, et kui x ja y on vastused, siis y ≡ x (mod 56), ning kui x on vastus ja y ≡ x (mod 56), siis ka y on vastus.
Küsime nüüd, kas funktsioonil T on püsipunkte, ehk kas leidub x, nii et T(x) = x? Saame lineaarse võrrandi, mille ühene lahend on x = -4.
Olgugi, et -4 ei ole antud kontekstis ülesande vastuseks, on see siiski vastus, sest vastuse definitsioon ei välista negatiivseid täisarve. Eelneva põhjal on iga täisarv y, mille korral y ≡ -4 (mod 56), vastuseks. Vähim selline naturaalarv on -4 + 56, ehk 15621.
Väikseim käbide arv on 15621
Jõulukontserdi eel kohtas üks eelnevalt julgust kogunud lauljapäkapikk teise küla päkapikukoori ja laulis tervituseks: „Olge tervitatud, 100 päkapikku!“ Kooripresident, vana ja väärikas päkapikk, aga vastas talle: „Ei, kullake, meid pole sada päkapikku!
Aga kui meid oleks nii palju, kui meid on, ja veel nii palju, ja veel pool nii palju, ja veel veerand nii palju, ning kui sina, päkapikk, oleksid ka meiega, siis alles oleks meid sada.
Aga nüüd… noh, eks sa rehkenda ise, kui palju meid on.“
Tähistame veerand koori tähega x, terve koor on siis 4x ja pool koori 2x.
4x +4x +2x +x =99, seega 11x =99 ja x =9
Päkapikukooris on 36 lauljat.
Ühel päeval sigines töökate päkapikkude hulka Laiskvorst-päkapikk. Õppida ta ei viitsinud, töö juures viilis nii palju, kui vähegi võimalik, kuid raha armastas ta väga ja oli sellele üsna maias. Ta ei tahtnud kuidagi aru saada, et ainult see raha omab väärtust, mis on ausa tööga teenitud.
Laiskvorst-päkapikk lonkis kord tegevuseta ringi ja ohkis: „Oh seda mu kibedat saatust küll! Keegi ei taha mind enam tuttavakski pidada. Muudkui aga räägivad: „Laiskvorste pole meil tarvis. Sa ei tee ise mitte midagi ega lase ka meil kibekiirel tööajal korralikult kingitusi meisterdada. Käige…!” Kas mõni härjapõlvlane suudaks mulle head nõu anda, kuidas rikkaks saada?”
Vaevalt jõudis Laiskvorst-päkapikk niiviisi mõelda, kui juba oligi eriti pika habemega härjapõlvlane kohal. „Noh, kui sa just tahad, siis ma aitan sind. Töö on kerge ja rikkaks saad sa ka. Kas näed seda silda seal eemal?”
„Näen,” vastas pisut araks löönud Laiskvorst.
„Noh, mine siis mööda seda silda jõe teisele kaldale, ja niipea kui sa sinna jõuad, ongi sul taskus kaks korda rohkem raha kui enne. Ja nii iga kord – niipea kui sa lähed üle silla, on sul raha kaks korda rohkem kui enne.”
„Kas tõesti?” rõõmustas Laiskvorst-päkapikk.
„Ausõna!” kinnitas härjapõlvlane. „Mul on ainult üks tingimus. Selle eest, et ma sulle niisuguse heateo teen, pead sa iga kord mulle üle silla minnes andma 24 kuldraha.”
„Noh, mis siis ikka,” nõustus Laiskvorst. „Kui raha iga korraga kahekordistub, miks siis neid kuldmünte keelata. Minu pärast võib kas või kohe peale hakata.”
Laiskvorst läks prooviks korra üle silla, luges oma raha üle, ja ennäe imet – raha oli tõesti poole rohkem kui enne. Ta viskas härjapõlvlasele 24 kuldraha ja läks teist korda üle silla. Raha oli jälle kaks korda rohkem kui enne. Laiskvorst andis härjapõlvlasele 24 kuldraha ja astus kolmandat korda üle silla. Raha hulk muidugi kahekordistus, kuid oh õnnetust – seda oli nüüd täpselt 24 kuldraha, parajasti just nii palju, et jätkus härjapõlvlasele võla tasumiseks. Härjapõlvlane kihistas õelat naeru ja kadus Laiskvorsti silmist.
Laiskvorst jäi nii oma viimasestki rahast ilma. Nagu näha, ei tohi alati võõrast nõuannet uskuda; tuleb ise kah üht-teist osata!
Kui palju oli Laiskvorst-päkapikul alguses raha?Selle ülesande lahendamist alusta lõpust, arvesse võttes seda, et pärast kolmandat silla ületamist oli Laiskvorstil täpselt 24 kuldmünti, mis ta pidi ära andma. Kui Laiskvorstil pärast viimast silla ületamist oli täpselt 24 küldmünti, siis enne seda oli tal järelikult 12 kuldmünti. Need kaksteist kuldmünti jäid talle taskusse pärast seda, kui ta andis ära 24 münti. Seega pärast teist silla ületamist oli tal taskus 36 kuldmünti. Järelikult teist korda asus ta silda ületama 18 münti taskus, kusjuures need 18 münti jäid talle taskusse pärast seda, kui ta läks esimest korda üle silla ja andis ära 24 kuldmünti. Tähendab, pärast esimest üleminekut oli tal 18 + 24 = 42 kuldmünti. Siit selgub, et alguses oli Laiskvorstil taskus 21 kuldmünti
Laiskvorst-päkapikul oli alguses 21 kuldmünti.
Matemaatika-Päkapikk palus tuttavaks saanud päkapikuneiult tema telefoninumbrit. Päkapikuneiu aga tahtis enne matemaatikut testida. Ta mõtles korraks ja ütles: „Kabinetis, kus ma töötan, on neli telefoni. Kui sa need numbrid ära arvad, siis annan sulle enda isikliku numbri. Aga nüüd pane hästi tähele.
Üheski mu kabineti telefoninumbris ei ole korduvaid numbreid, kuid neil on ühine omadus – iga telefoninumbri numbrite summa on 10. Kui aga telefoninumbrile liita arv, mis on vaadeldavast telefoninumbrist vastupidises järjekorras, tekib kõigil neljal juhul üks ja seesama arv, mis koosneb vaid ühesugustest numbritest.
Lisaks arvesta sellega, et linnas, kus päkapikuneiu töötab, on telefoninumbrid vahemikus 20 000 kuni 99 999.
Kui sa peaksid paari päeva pärast mind taas siin Jõulumaa kohvikus lõuna ajal trehvama ja tead kõiki neid numbreid, siis annan sulle oma telefoninumbri.“
Esita kasvavas järjekorras päkapikuneiu kabineti 4 telefoninumbrit.Kuna otsitavates telefoninumbrites ei ole korduvaid numbreid ja neid on üldse viis ning kuna nende summa on 10, siis telefoninumbrid koosnevad numbritest 0, 1, 2, 3 ja 4 (kõlk teised võimalused annavad telefoninumbri numbrite summaks 10-st suurema arvu).
Olgu üks telefoninumber abcde. Et {a; b; c; d; e} = {0; 1; 2; 3; 4), siis summa abcde+ edcba ei saa olla kuuekohaline arv.
Olgu abcde + edcba =kkkkk. Arvestades, et ükski number a, b, c, d, e ei ületa arvu 4, siis a + e + b + d = 2c = k. Siit 5k = 2( a + b + c + d + e) = 20, sest a + b + c + d + e = 10. Seega k = 4 ja Jarelikult c = 2. Kuna otsitavad telefoninumbrid on suuremad kui 20000, siis saab olla a = 3 või a = 4. Kui a = 3, siis e = 1 (a + e = k = 4) ning b = 0 ja d = 4 või b = 4 ja d = 0 (need väärtused rahuldavad tingimust b + d = k = 4). Kui a = 4, siis e - 0 ning b = 1 ja d = 3 või b = 3 ja d = 1.
Seega telefoninumbrid, mis rahuldavad ülesande tingimusi,on 30241, 34201, 41230, 43210.
Päkapikuneiu kabineti telefoninumbrid: 30241, 34201, 41230, 43210
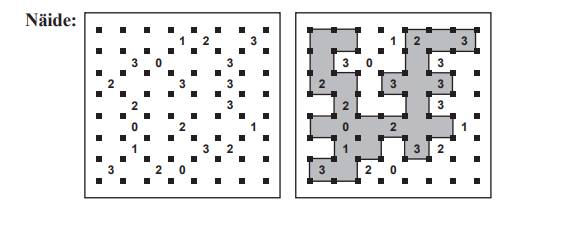
Päkapikkudel on käsil „müürimõistatuste” lahendamise õhtu. Mõistatuses tuleb neil ehitada vertikaal- ja horisontaalsuunas jooni tõmmmates „müür”. Mõistatuses olevad numbrid näitavad, mitu joont tuleb numbri ümber joonistada, et müür kokku saada. Lõpuks peab moodustuma üks terviklik müür, st eraldi asuvaid „müüriosi“ ei tohi olla.
Vastuseks on numbrid, mis jäävad müürist väljapoole, alustades ülalt vasakult. Näites on vastuseks 1,303,3,1,2,20
Päkapikud lahendasid järgnevat müürimõistatust:

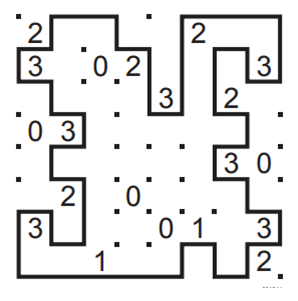
2,32,03,30,2,2
Ülesanne pärineb 2016. aasta loogikamõistatuste lahendamise Eesti koondise valikvõistluste ülesannetest. Kõigi sealsete ülesannetega saab tutvuda kuma.ee lehel rubriigis "Võistlused". Suur tänu, et lubasite seda ülesannet matemaatilises advendikalendris kasutada!
Uueks aastaks kinkis Jõuluvana oma kolmele pojale nii mitu hõberaha, kui vana igaüks oli. Kokku kinkis ta 24 hõberaha, kuid kingitust üle andes ütles: „Las kõige noorem teist jätab poole saadud rahast endale, ülejäänu aga jagab vendade vahel pooleks. Las keskmine poeg jätab poole rahast, mis tal seejärel on, endale, ülejäänu jagab vendade vahel pooleks. Ja las lõpuks toimib niisamuti kõige vanem teist.“
Pärast niisugust jagamist oli kõigil vendadel ühepalju raha.
Kui vanad olid vennad?Alustame ülesande lahendamist lõpust. Jagamise lõpuks oli igal vennal 8 hõberaha. Vanemal vennal oli enne raha jagamist 2 korda rohkem raha kui lõpus, st 2 × 8 = 16 hõberaha. Vanem vend jagas teiste vendade vahel ära 16 - 8 = 8 hõberaha, mis tähendab, et keskmine ja noorem vend said vanemalt vennalt kumbki 4 hõberaha. Enne vanema venna hõberaha jagamist oli nii nooremal kui ka keskmisel vennal 8 - 4 = 4 hõberaha.
Enne vanema venna müntide jagamist oli seis:Keskmisel vennal oli enne raha jagamist 2 korda rohkem raha, st 2 × 4 = 8 hõberaha. Ta jagas 8 - 4 = 4 hõberaha vanema ja noorema vahel ära. Seega sai vanem 2 hõberaha ja noorem 2 hõberaha.
Enne keskmise venna raha jagamist oli seis:Nooremal vennal oli enne raha jagamist 2 korda vähem raha, st 2 × 2 = 4 hõberaha. Ta jagas vendade vahel 4 - 2 = 2 hõberaha, ehk kumbki vend sai 1 hõberaha.
Enne noorema venna raha jagamist oli seis:Vennad on 13 ja 7 ja 4 aastat vanad.
Sajast päkapikust õpib ainult saksa keelt 18, saksa keelt ja mitte inglise keelt 23, saksa keelt ja prantsuse keelt 8, saksa keelt kokku 26, prantsuse keelt kokku 48, prantsuse ja inglise keelt 8 ning mitte ühtegi keelt 24 päkapikku.
Mitu päkapikku õpib inglise keelt? Mitu päkapikku õpib saksa ja inglise keelt, kuid mitte prantsuse keelt?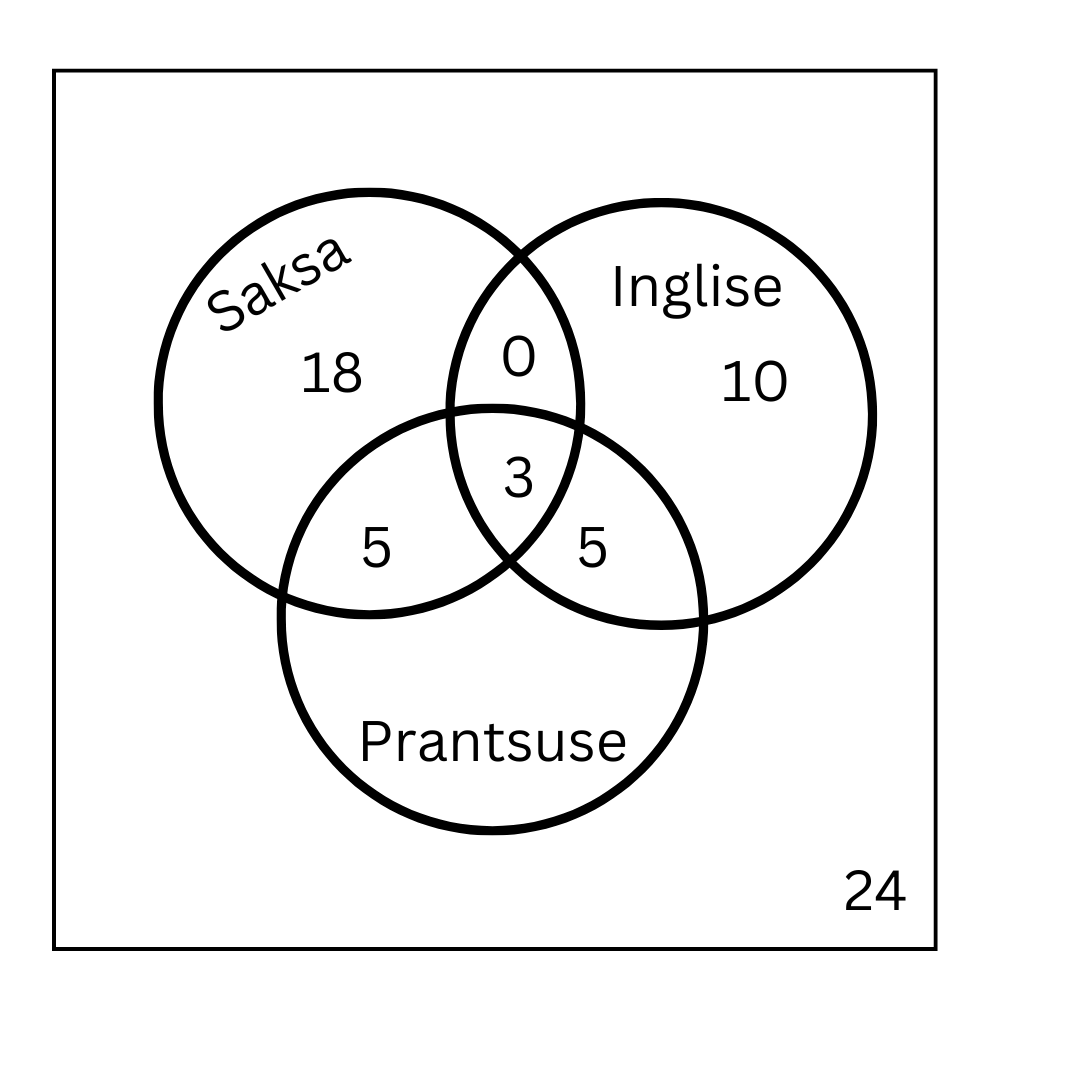
Inglise keelt õpib 18 päkapikku. Saksa ja inglise keelt, kuid mitte prantsuse keelt õpib 0 päkapikku.
Päkapikud on Lume küla Helbekese tänaval jagamas kingitusi. Paraku on pimedal tänaval raske orienteeruda ning ainuke asi, mida nad näevad on, et tänaval on reas neli maja.
Kogenud Jõuluvana abiline sellest päkapikkude seltskonnast on selles tänavas varem korduvalt käinud, ja teda pime tänav ei heiduta. Selle asemel hakkab ta oma vähemkogenud kolleegidele vihjeid jagama.
Sellist tüüpi ülesannete lahendamisel on suureks abiks tabeli tegemine, kus tulbad tähistavad majade asukohti. Seejärel tuleb järjest vihjete abil hakata lahtreid täitma. Olenevalt sellest, kas alustad vasakult või paremalt poolt, on võimalik saada erinevad lahendused. Järgnevalt üks võimalik tulemus.
Jõuluküla ülemarvutuspäkapikk teeb laoruumis numbrite inventuuri ja vangutab pead. Äkitselt ütleb ta kõva häälega.
Nüüd teeb päkapikk väikese mõttepausi ja ütleb:
Siis mõtleb päkapikk uuesti ja ütleb:
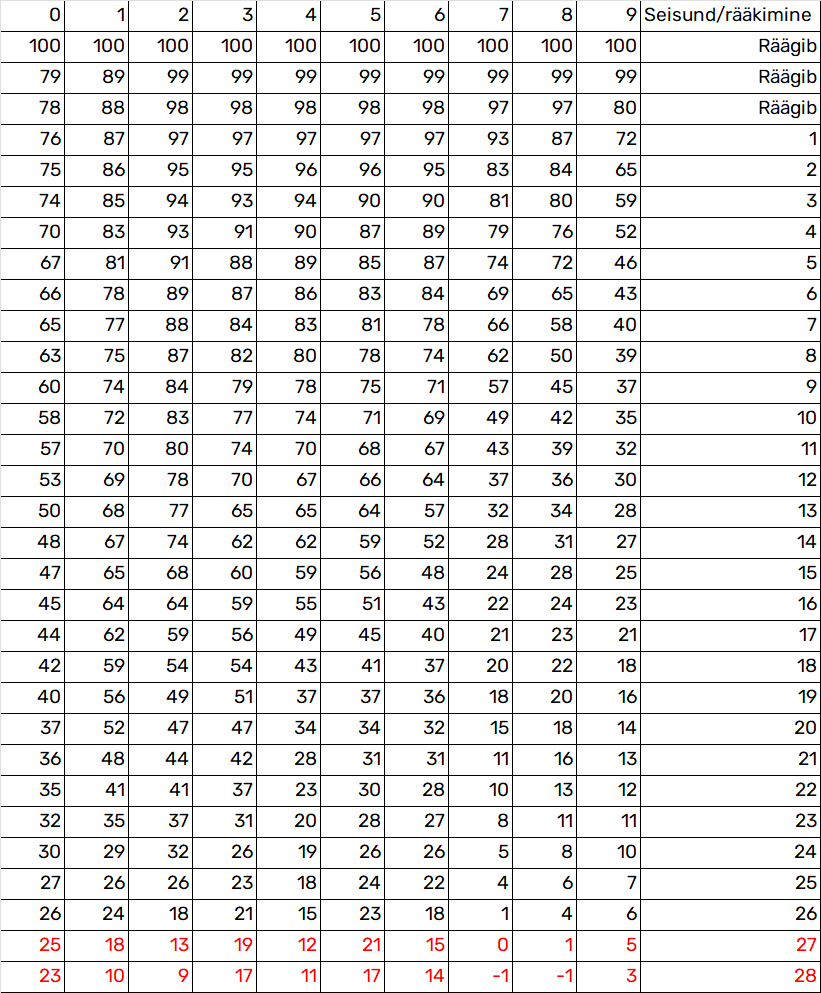
Ülemarvutuspäkapikk saab rääkida veel 26 korda. Pärast 26-ndat rääkimist on number 7 otsas.
Päkapikkude puhketoas oli üks kolmnurkne vaip. Päkapikud soovisid vaipa väiksemaks teha ning otsustasid valida vana vaiba külgede keskpunktid uue kolmnurkse vaiba tippudeks. Kui nad olid uue vaiba valmis saanud, märkasid nad, et tegu on affiinselt teisendatud versiooniga vanast vaibast. Huvitaval kombel oli vaibal üks punkt, mis jäi pärast affiinset teisendust paigale.
Milline punkt see oli?Mediaanide lõikepunkt/massikese.
Pakane on müstiline olend, kes elutseb kõrgemates ruumimõõtmetes. Päkapikukütt tahab Pakase kinni püüda. Püüdmiseks on vaja luua kõrgemõõtmelised 5×5×…×5 trellid, mis koosnevad d-dimensioonilistest kuubikutest. Kahjuks ei mäleta päkapikukütt, mis mõõtmelisi kuubikuid oli selleks vaja. Samas mäletab ta, et vajaminevate kuubikute arv oli vähemalt 138×1012 ja mitte rohkem kui 570×1012
Juhised trellide moodustamiseks:
Kui kuupide asukohti vaadata koordinaatidena (x1, x2 ,x3, …, xd), kus x1, …, xd võtavad väärtusi 1, 2, 3, 4, 5 siis trellides paiknevad d-mõõtmelised kuubid parajasti nendel kohtadel, kus vähemalt d-1 koordinaati on paarisarvud.
Vaatame kahte juhtu.
Seega kokku on meil 2d + 3d 2(d-1) = (3d+2)2(d-1) kuubikut.
Sellisest funktsioonist pöördfunktsiooni võtmine on keeruline. Selle asemel me saame kasutada log2 funktsiooni, mis annab ligilähedase tulemuse, kuid hindab üle, ja siis lihtsalt proovida eelnevalt tuletatud valemit erinevate arvudega.
Vaja läheb 42 mõõtmelisi kuubikuid
Aasta lõpp tähendab Päkapikukülas eelarvejäägi kulutamist. Laoosakonna päkapikud soovivad endale uut kangkaalu ja uusi kaaluvihte. Kaaluga peaks olema võimalik kaaluda kõiki täisarvulisi raskusi alates 1 kg kuni 40 kg. Kuna kaaluvihikute ostmine on kallis, soovib eelarvepäkapikk osta vähima arvu vihte.
NB! Kaaluvihte võib asetada mõlemale kaalukausile. Näiteks kui sul on 5 kg ja 7 kg kaaluvihid, saad kaaluda ka 2 kg eset, asetades 5 kg kaaluvihi samale kausile ning 7 kg kaaluvihi teisele kausile.
Mis vihid peaks päkapikk laoosakonda ostma?Alustame lahenduskäiku sellega, et kaaluda saame ainult kaaluvihtide abil, mille väärtused on a ja b, kus a < b. Kui meil on kaks kaaluvihti a ja b, siis saame kaaluda järgmisi raskusi:
b a b-a a+b
Seega saame kaaluda raskusi 1 kg kuni 4 kg. On lihtne kontrollida, et sobivad kaaluvihed on a = 3 ja b = 1. Kui lisame kolmanda kaaluviha, tekivad järgmised kombinatsioonid:
1 3 - 1 3 3 + 1 c - 3 c - (3 - 1) c - 1 c c + 1 c + (3 - 1) c + 3
Näeme, et saame kaaluda kolmteist raskust, kusjuures c = 9
Kui jätkame analoogselt, saame kaaluda kokku 40 raskust nelja kaaluvihega: 1, 3, 9 ja 27.
Päkapikk peaks laoosakonda ostma järgnevad kaaluvihid (kg): 1,3,9,27
Jõulutehases läks pakkimismasin rikki ja pakkepaelast tekkis suur pundar. Rikke parandamiseks on vaja pundar manuaalselt lahti harutada. Selleks saad opereerida kahe kangiga V(ääna) ja P(ööra). Masina kõrvalt leiad käsiraamatu, mis seletab kangide operatsiooni.
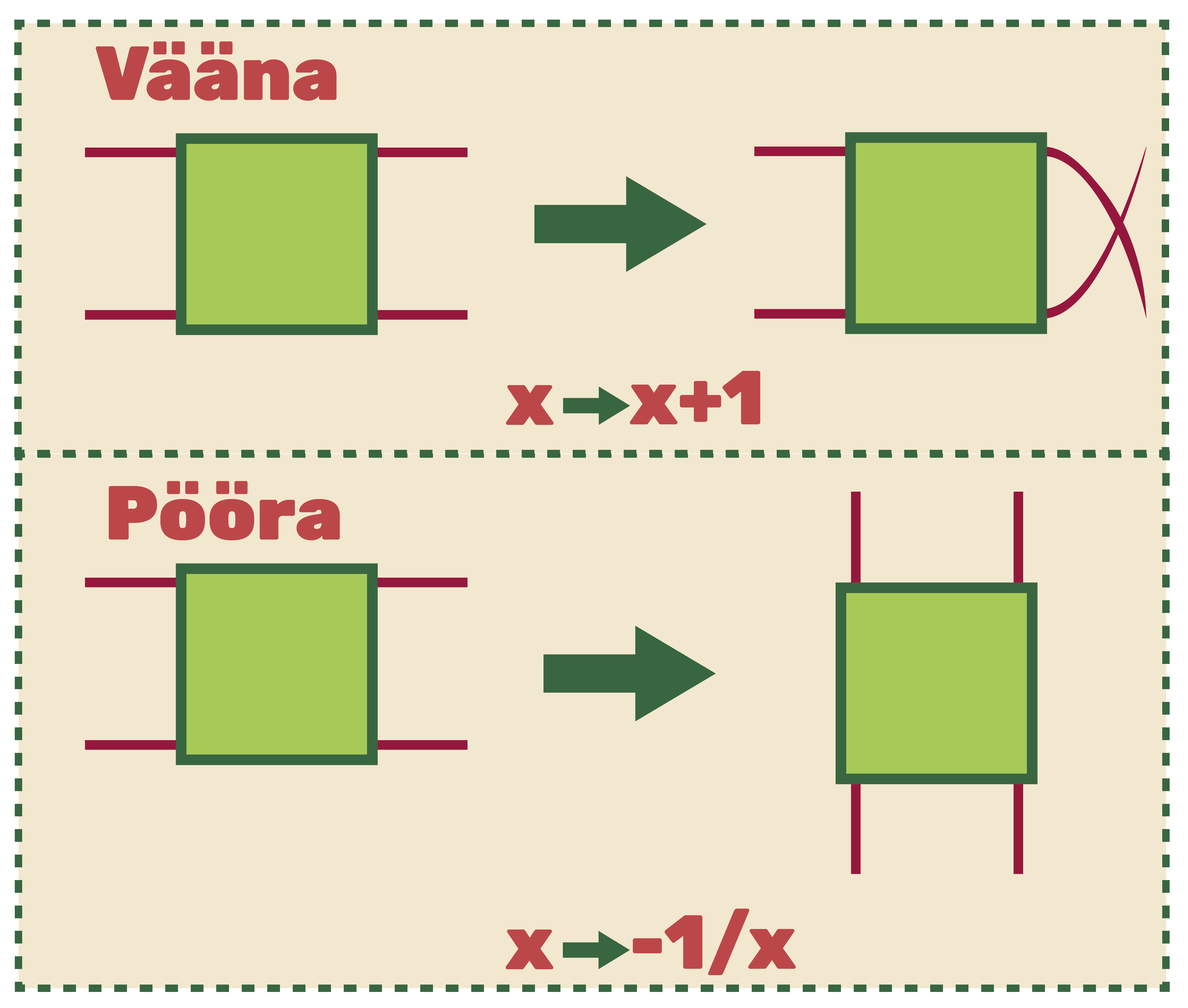
Lisaks edastab masin veateatena arvu 25/57, mis tähistab kangidega opereerimisel tekkinud väärtust (vaata tabelit allpool)
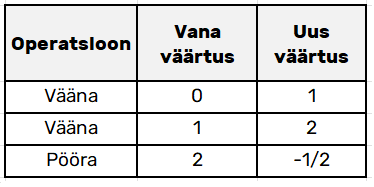
Sellel ülesandel on mitu õiget lahendust ja loeme õigeks kõik, mis annavad õige tulemuse. Üks võimalik lahendustest on antud tabelis.
Olgu meil antud murd a/b, kus 0<a<b. Kasutame operatsiooni Pööra, ning sellest saab murd -b/a. Nüüd rakendame k-korda operatsiooni Vääna, kus 0≤ ka-b<a. Jätkata nii kaua kuni väärtus on 0.